Методы Монте-Карло в прикладной математике и вычислительной аэродинамике

Академик О.М. Белоцерковский, ИАП РАН,

Профессор Ю.И. Хлопков, ЦАГИ

Аннотация. В работе излагается обзор методов Монте-Карло, разработанных в вычислительной аэродинамике разреженного газа, и их применение в смежных, нетрадиционных для использования статистического моделирования, областях. Приводится краткая история развития методов, их основные свойства, достоинства и недостатки. Устанавливается связь прямого статистического моделирования аэродинамических процессов с решением кинетических уравнений и показывается, что современный этап развития вычислительных методов немыслим без комплексного подхода к разработке алгоритмов с учётом всех особеннстей решаемой задачи: физической природы процесса, математической модели, теории вычислительной математики и стохастических процессов. Рассматриваются возможные пути развития методов статистического моделирования.

1. Введение. Проявление методов статистического моделирования (Монте-Карло) в различных областях прикладной математики, как правило, связано с необходимостью решения качественно новых задач, возникающих из потребностей практики. Так было при создании атомного оружия, на первом этапе освоения космоса, исследовании явлений атмосферной оптики, физической химии, моделировании турбулентности. В качестве одного из более-менее удачных определений методов Монте-Карло можно привести следующее:

Методы Монте-Карло – это численные методы решения математических задач (систем алгебраических, дифференциальных, интегральных уравнений) и прямое статистическое моделирование (физических, химических, биологических, экономических, социальных процессов) при помощи получения и преобразования случайных чисел.

Первая работа по использованию метода Монте-Карло была опубликована Холлом [1] в 1873 году именно при организации стохастического процесса экспериментального определения числа путём бросания иглы на лист линованной бумаги. Яркий пример использования методов Монте-Карло – использование идеи Дж. фон Неймана при моделировании траекторий нейтронов в лаборатории Лос Аламоса в сороковых годах прошлого столетия. Хотя методы Монте-Карло связаны с большим количеством вычислений, отсутствие электронной вычислительной техники ни в том ни в другом случае не смутило исследователей при применении этих методов, поскольку в том и другом случае речь шла о моделировании случайных процессов. И своё романтическое название они получили по имени столицы княжества Монако, знаменитой своими игорными домами, основу которых составляет рулетка – совершенный инструмент для получения случайных чисел. А первая работа, где этот вопрос излагался систематически, опубликована в 1949 году Метрополисом и Уламом [2], где метод Монте-Карло применялся для решения линейных интегральных уравнений, в котором явно угадывалось задача о прохождении нейтронов через вещество. В нашей стране работы по методам Монте-Карло стали активно публиковаться после Международной Женвской конференции по применению атомной энергии в мирных целях. Одной из первых можно привести работу Владимирова и Соболя [3].

Общая схема метода Монте-Карло основана на Центральной предельной теореме теории вероятности, утверждающей, что случайная величина , равная сумме большого количества N произвольных случайных величин с одинаковыми математическими ожиданиями m и дисперсиями , всегда распределена по нормальному закону с математическим ожиданием и дисперсией . Предположим, что нам нужно найти решение какого либо уравнения или результат какого либо процесса I. Если сконструировать случайную величину с плотностью вероятности таким образом, чтобы математическое ожидание этой величины равнялось искомому решению , то это даёт простой способ оценки решения и погрешности

Отсюда следуют общие свойства методов:

- абсолютная сходимость к решению, как ;

- тяжёлая зависимость погрешности от числа испытаний, как (для уменьшения погрешности на порядок, необходимо увеличить количество испытаний на два порядка);

- основным методом уменьшения погрешности является максимальное уменьшение дисперсии, другими словами, максимально приблизить плотность вероятности p(x) случайной величины к математической формулировке задачи или физике моделируемого явления;

- погрешность не реагирует на размерность задачи (в конечно-разностных методах при переходе от одномерной задачи к трёхмерной количество вычислений увеличивается на два порядка, в то время как в методах Монте-Карло количество вычислений остаётся того же порядка);

- простая структура вычислительного алгоритма ( N раз повторяющиеся однотипные вычисления реализаций случайной величины);

- кроме того, конструкция случайной величины, вообще говоря, может основываться на физической природе процесса и не требовать обязательной, как в регулярных методах, формулировки уравнения, что для современных проблем становится всё более актуальным.

Основные свойства методов Монте-Карло и условия, при которых они уступают и превосходят традиционные конечно-разностные подходы, можно продемонстрировать на какой-нибудь простой задаче, например, на задаче о вычислении интеграла

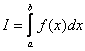
где x, a и b – вектора в n-мерном евклидовом пространстве. Случайную величину c плотностью р(x) сконструируем таким образом, чтобы её математическое ожидание

М() =

равнялось нашему интегралу I. Тогда, если в соответствующих пределах выбрать , то по Центральной предельной теореме

(1)

Итак, первое. Вычисление интеграла I можно трактовать как решение математически сформулированной задачи с одной стороны, и прямое моделирование определения объёма, находящегося под функцией f(x) c другой стороны.

Второе. Вычисление одномерного интеграла методом Монте-Карло соответствует вычислению I по методу прямоугольников с шагом и погрешностью О(). В принципе, при достаточно хорошей функции в одномерном случае, не увеличивая существенно количество вычислений, интеграл можно вычислять с точностью О() по трапециям, с точностью О() по параболам и, вообще, с любой точностью. В многомерном случае трудности использования схем высокого порядка становятся настолько существенными, что при вычислении n-мерных интегралов при n редко используются схемы высокого порядка.

Проведём соответствие между эффективностью регулярных и статистических методов. Пусть n – размерность задачи, Y – число узлов на оси, - общее число узлов для регулярных методов, q – порядок точности схемы, N – число статистических испытаний, - количество операций обработки одного узла, - погрешность вычислений для регулярных методов, - погрешность вычислений для статистических методов, = = - количество операций при решении задачи регулярными методами, = - количество операций по методу Монте-Карло. В случае одинакового количества операций при вычислении решения тем и другим методом с одинаковой точностью мы получаем соотношение

Это означает, что при где в основном используются схемы первого порядка, методы Монте-Карло становятся предпочтительней.

2. Особое место методы Монте-Карло занимают в вычислительной аэродинамике.

Динамика разреженных газов описывается известным интегродифференциальным кинетическим уравнением Больцмана

(2)

- функция распределения молекул по времени, координатам и скоростям.

- функции распределения, соответствующие скоростям молекул после столкновения .

- относительные скорости молекул при парных столкновениях .

- прицельное расстояние и азимутальные угол при столкновениях частиц.

Сложная нелинейная структура интеграла столкновения и большое количество переменных (в общем случае - 7) создают существенные трудности для анализа, в том числе и численного и практически исключают конечно-разностный подход для серьёзных задач. И, в тоже время, многомерность и вероятностная природа кинетических процессов создают естественные предпосылки для применения методов Монте-Карло. Исторически развитие численных статистических методов в динамике разреженных газов шло по следующим трем направлениям:

- использование методов Монте-Карло для вычисления интегралов столкновения в регулярных конечно-разностнных схемах решения кинетических уравнений;

- прямое статистическое моделирование физического явления, которое разделяется на два подхода: моделирование траекторий «пробных частиц» по Хэвиленду [4] и моделирование эволюции «ансамбля частиц» по Бёрду [5];

- построение случайного процесса типа процедуры Уалама-Неймана, описанной в [6], соответствующего решению кинетического уравнения.

Вероятностная природа аэродинамики разреженных газов так важная для применения и разработки численных схем Монте-Карло естественным образом следует из общих принципов кинетической теории и статистической физики. Приведённые ниже рассуждения также вполне можно рассматривать и как уровни тщательности описания динамики большой молекулярной системы, которые в дальнейшем нам понадобятся для конструирования эффективных методов статистического моделирования.

Наиболее подробным уровнем описания является динамическая система. Для описания такой системы, состоящей из большого количества элементов , (а молекулярный газ и является такой системой с молекул) необходимо задать начальные координаты и скорости каждой молекулы () и уравнения эволюции этой системы

(3)

Решение подобной системы является совершенно нереальной задачей даже для очень разреженного газа – на высоте 400 км (наиболее популярные орбиты для спутников) в одном кубическом см содержится молекул. Поэтому переходят к менее полному - статистическому описанию поведения системы.

Следуя формализму Гиббса, рассматривают не одну систему, а ансамбль

систем в 6N-мерном Г-пространстве, распределённых в соответствие с N-частичной функцией распределения , имеющей смысл вероятности нахождения системы

в момент времени t в точке в окрестности

Подобный ансамбль описывается известным уравнением Лиувилля

(4)

И вот с этого момента уравнение Лиувилля и все последующие кинетические уравнения, следующие из цепочки Боголюбова, включая последнее её звено - уравнение Больцмана, имеют вероятностную природу. И хотя уравнение (4) проще системы (3), оно учитывает N-частичные столкновения молекул и также чрезвычайно сложно для практического анализа. Переход на менее детальный уровень описания связан с дальнейшим огрублением описания системы с помощью s- частичных функций распределения , определяющих вероятность одновременного обнаружения s частиц независимо от состояния остальных N-s частиц.

Следуя идеям Боголюбова, получают цепочку зацепляющихся уравнений

, (5)

вплоть до одно-частичной функции распределения газа Больцмана с учётом лишь парных столкновений

Следуя Больцману, будем считать молекулы сферически симметричными и принимая гипотезу молекулярного хаоса, приходим к уравнению (2).

Весьма интересным представляется частный случай уравнения Лиувилля (4) и цепочки Боголюбова (5) пространственно-однородного рассмотрения газа, состоящего из ограниченного числа частиц, который на конечном звене, соответствующего двухчастичным столкновениям, приводит к известному уравнению Каца «Master Equation» [7]

(6)

где - одно и двух частичные функции распределения. В отличие от уравнения Больцмана, уравнение (6) является линейным, что и будет использовано при присоздании и обосновании эффективных численных схем прямого статистического моделирования.

Возвращаясь к уравнению Больцмана, из определения функции f легко выводятся все макроскопические параметры. Так число молекул n в объеме единицы газа равно

.

Точно так же средняя скорость молекул, тензор напряжений, и вектор потока энергии определяются отношениями:

,

,

.

где тепловая скорость молекул.

Средняя энергия теплового движения молекул обычно характеризуется температурой

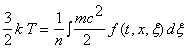
Применяя к уравнению Больцмана процедуру Энскога-Чепмена, получают гидродинамический уровень описания. Это уровень описания системой уравнений Навье-Стокса

,

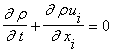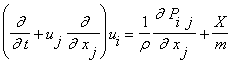
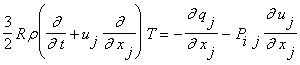₍₇₎

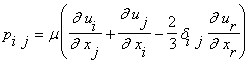
и уравнений Эйлера

,

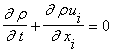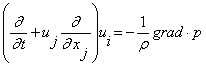₍₈₎

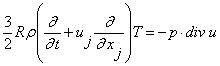
Следуя общей логике изложения, можно предположить, что и динамика сплошной среды как частный сучай кинетического рассмотрения движения газа, имеет черты статистической природы и допускает статистическое моделирование, что и будет показано ниже.

3. Построение эффективных методов статистического моделирования.

Центральное место в динамике разреженных газов, безусловно, занимают методы прямого статистического моделиpования и работы по констpуиpованию статистических процедур при прямом моделировании открыли широкие возможности по повышению эффективности методов, снижая, буквально на порядки быстодействие и объем оперативной памяти ЭВМ, по сравнению с первоначальными модификациями, что позволило их применять к решению двухмерных и, в последствии, с учетом pеальных свойств газов трехмерных задач. Однако при исследовании и обосновании применения этих методов фактически невозможно обойтись без рассмотрения описывающего моделируемое явление кинетического уравнения. Установление связи статистической процедуры с решением кинетического уравнения является необходимым по целому ряду причин. Во-первых, для того чтобы доверять решению и использовать полученные результаты в качестве эталонных, поскольку решения многих характерных задач были впервые решены именно методами прямого моделирования и до сих пор не повторены другими методами. Во-вторых, установление соответствия моделирования решению уравнения позволяет использовать хорошо развитый аппарат численных регулярных и статистических методов решения уравнений математической физики для анализа и повышения эффективности методов. И в-третьих, это позволяет установить некоторый общий подход к построению методов и исключает всякого рода ложные модификации.

Следует подчеркнуть, что сложность практических задач высотной гиперзвуковой аэродинамики для разработки эффективных численных алгоритмов с необходимостью требует привлечения всего арсенала теоретических, экспериментальных, численных методик исследования течений разреженного газа. В этой связи особую значимость преобретает анализ кинетического уравнения и исследование его различных моделей. Часто пользуются приближенными представлениями интеграла столкновений и функции распределения. Наиболее распространенными приближенными формами кинетических уравнений являются:

- модельное уравнение Крука [8]

, (9)

где -частота столкновений, 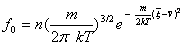- равновесная функция распределения;

-эллипсиодальная модель Халвея

,

- эллипсиодальная функция распределения;

-аппроксиомационная модель Шахова [9], которая в отличие от предыдущих моделей даёт правильное число Пpантля

, , , (10)

- безpазмеpная молекулярная тепловая скорость.

Здесь же необходимо упомянуть линеаризированое уравнение Больцмана, которое строго выводится из полного уравнения Больцмана при условии, что функция распределения слабо отличается от равновесной

(11)

где и - некоторые известные функции молекулярных скоростей, зависящие от сорта частиц.

Модельные уравнения в отличие от линеаризованного не следуют строго из уравнения Больцмана, кроме того являются существенно более нелинейными, чем исходное уравнение, но в практической реализации при численном моделировании могут оказаться проще.

В практической реализации методы прямого статистического моделирования, основанные на подходах Бёрда и Хэвиленда, естественно, оказались наиболее эффективными и их модификации с переменным успехом осуществляли победное шествие по вычислительной аэродинамике.

К настоящему времени безусловнный приоритет в динамике разреженного газа принадлежит методу Бёрда, модификации которого трудами отечественных исследователей О. Белоцерковского, В. Яницкого, М. Иванова, В. Перепухова, А. Ерофеева [10-21] позволили буквально на порядки повысить эффективность метода. Суть метода заключается в том, что эволюция системы на малом промежутке времени ращепляется на два ясных физических процесса: 1) релаксацию в соответствии с оператором столкновений в кинетическом уравнении

2) свободно-молекуляный перенос (12)

Это хорошо известная схема ращепления первого порядка по для любого операторного уравнения, но в данном случае она подкупает тем, что ращепляет динамику такой сложной кинетической системы на два ясных физичеких процесса. Функция распределения моделируется N частицами, которые на первом этапе в кажлой ячейке между собой сталкиваются в соответсвии с частотой столкновения на протяжени времени , а на втором, в течении , перелетают на расстояния .

Центральным местом в методе нестационарного статистического моделирования является процедура подсчета столкновений. Пара частиц выбирается для столкновения в соответствии с частотой столкновений молекул, вне зависимости от расстояния между ними в данной ячейке. Скорости частиц после столкновения выбираются в соответствии с законами взаимодействия молекул. Хотя эффективность метода зависит от довольно многих параметров схемы счета (установления, расщепления по времени, выхода на стационарный режим, шага по времени, сетки по пространству и т.д.) основные работы по совершенствованию метода посвящены улучшению процедуры столкновений и уменьшению статистической погрешности схемы, как основного момента, позволяющего уменьшить количество частиц в ячейках и, соответственно, уменьшить оперативную память вычислительной машины и уменьшить время расчёта. Так в работе [18] была предложена модификация процедуры столкновений для одного частного случая - масквелловских молекул, при которой результаты расчета практически не зависят от количества частиц в ячейке при их изменении от 40 до 6. (При обычных расчетах количество частиц в ячейках порядка 30). В работах [11-16] предложен общий метод, независящий от сорта молекул, в котором на этапе столкновений подсистема частиц в каждой ячейке рассматривается как N-частичная модель Каца(6)

Моделирование столкновения сводится к статистической реализации эволюции не уравнения Больцмана (2), а модели Каца (6) в течении времени t. Время столкновения в модели Каца рассчитывается в соответствии со статистикой столкновения в идеальном газе по схеме Бенулли. Эта схема позволяет использовать существенно меньшее число частиц в ячейке и более мелкий шаг расчетной сетки. Анализ результатов показал, что результаты расчета практически не зависят от количества частиц в ячейке вплоть до 2. Дело в том, что уравнение Больцмана с необходимостью требует предположения о молекулярном хаосе, которое при том количестве частиц в ячейке, на которое способны современные компьютеры, выполняется с систематической ошибкой, уравнение (6) этого не требует и поэтому этап столкновения рассчитывается как чисто марковский процесс. А с другой стороны, при имеет место полная эквивалентность модели Каца и пространственно-однородного уравнения Больцмана. Таким образом, разработанный Белоцерковским – Яницким подход: 1) даёт путь построения эффективных численных схем, обеспечивающих возможность решения трёхмерных задач аэродинамического обтекания;

2) решает важнейшую методологическую задачу эквивалентности численного метода решению кинетического уравнения.

Методам традиционного использования статистического моделирования посвящено огромное количество работ, поэтому мы ограничимся в основном задачам аэродинамики. Как уже отмечалось, в практической реализации для задач динамики разреженных газов статистические методы оказались более эффективными по сравнению с регулярными и полурегулярными методами. Для задач обтекания, как наиболее существенных в аэродинамике, они впервые были успешно применены для получения аэродинамических характеристик различных, в том числе и сложных, тел, в свободномолекулярном и близком к свободномолекулярному потоках. Разработанная более двух десятков лет назад методика в настоящее время доведена до стандартных программ и широко используется в соответствующих проектных и конструкторских организациях. Продвижение в область меньших Kn связано с резким увеличением вычислительных трудностей, обусловленных уменьшением длины пробега молекул и, соответственно, более мелким шагом по времени и пространству и, в случае прямого моделирования, увеличением количества частиц, моделирующих функцию распределения.

Описанный выше метод позволил перейти к расчёту аэродинамических характеристик реальных компоновок. На фигурах 1-4 представлены характерные формы гиперзвуковых летательных аппаратов.

Фиг. 1 Типичная схема космического челнока

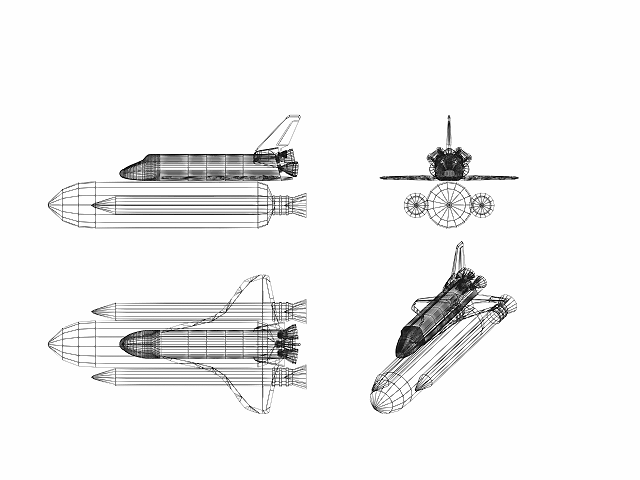
Фиг. 2 Система Энергия - Буран

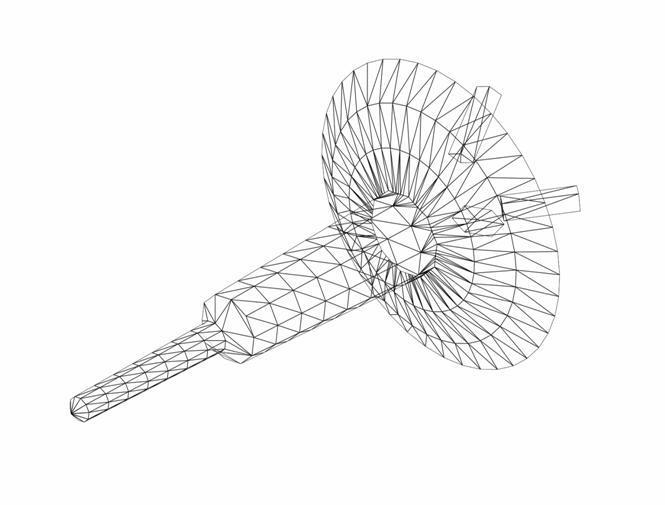
Фиг. 3 Марсианский пенетратор

Фиг. 4 Перспективный гиперзвуковой летательный аппарат

В качестве примера расчета аэродинамических характеристик на фигуре 5 представлено сопротивление гиперзвукового летательного аппарата, изображенного на фигуре 1 при различных режимах разреженности среды (число Рейнольдса - Re) и ориентации (углах атаки - .

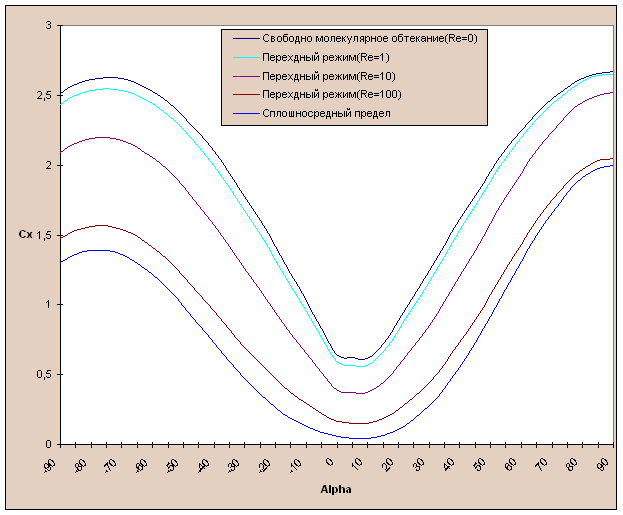
Фиг. 5 Коффициент сопротивления ВКС в зависимости от угла атаки

Как уже отмечалось, к настоящему времени несомненный приоритет во всём мире имеют современные методы, основанные на подходе Бёрда моделирования динамики «ансамбля молекул». Но так было не всегда. Одно время приоритет имели методы статистического моделирования «пробных частиц», основанные на подходе Хэвиленда. Возможно, в будущем появятся его эффективные схемы, как это уже было раньше, когда ещё не было тех эффективных схем подхода Бёрда, о которых речь шла выше. Или новый класс задач, для которых эти схемы станут приоритетными. Но уже сейчас можно выделить некоторые проблемы физической химии, для которых метод пробных частиц оказывается предпочтительнее. Но и, конечно, это класс линейных задач, с которых он, собственно, и начинался [2]. Есть ещё одно явное преимущество этого метода, которое состоит в том, что для него, в отличие от метода Бёрда, так остро проблема соответствия решению кинетического уравнения не стоит. Что касается вычислительной аэродинамики, то он основан на линеаризованном уравнении Больцмана (11).

4. Линейные задачи вычислительной аэродинамики. Следуя работе [22], рассмотрим течения, слабо отклоняющиеся от равновесных. В этом случае функцию распределения можно представить в виде:

,

где

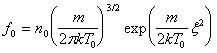
и уравнение Больцмана линеаризируется к виду (11):

(11)

здесь

Аналитические выражения для молекул, взаимодействующих по закону твердых сфер, имеют форму:

где , a и B - постоянные коэффициенты.

Интегрируя уравнение (11) вдоль траекторий, приходим к линейному интегральному уравнению:

где

к которому применима статистическая процедура Улама-Неймана [2].

В общем случае расчет методом Монте-Карло сводится к вычислению интегралов. Этими интегралами являются математические ожидания случайных величин, используемых в качестве оценок, другими словами производится оценка интеграла типа Лебега-Стильтьеса по некоторой вероятной мере

с помощью среднего арифметического по количеству испытаний

В случае pешения интегральных уравнений интеграл представляет собой функционал от решения уравнения

где D есть область S - мерного евклидова пространства , ;

и - функции, определенные в D, ядро - определено на декартовом произведении D на себя и интеграл в уравнении понимается в смысле Лебега. Решение такого уравнения дается сходящимся рядом Неймана:

где

В этом случае искомый функционал представляется в виде суммы кратных интегралов:

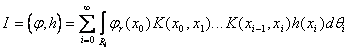
где , , ,

Обычно с исходным интегральным уравнением связывают однородную цепь Маркова, заданную плотность начального распределения и переходной плотностью . Выборочная траектория цепи строится в соответствии с начальной и переходной плотностями вероятности.

Тогда оценка искомого функционала будет иметь вид:

где

,

n - количество столкновений в траектории.

Таким образом, зная аналитическое выражение ядра, можно строить простой алгоритм вычисления различных функционалов решения интегрального уравнения.

При численном решении кинетического уравнения в качестве цепи Маркова рассматриваются траектории молекул (пробных частиц) на равновесной функции распределения. В этом случае используем простой процесс розыгрыша траекторий, близких к истинным, что существенно уменьшает диспеpсию. Процесс моделирования случайной величины полностью эквивалентен методу последовательных приближений. И поэтому решение, полученное методом Монте-Карло, сходится к решению уравнения Больцмана.

На фигуре 7 представлено решение линеаризованного уравнения Больцмана для расчета коэффициента диффузии броуновской частицы и сравнение с экспериментальными результатами Милликена.

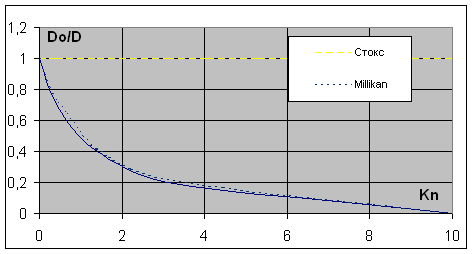
Фиг. 7 Коэффициент диффузии броуновской частицы в разреженном газе

5. Возможные направления развития методов вычислительной аэродинамики. Как уже отмечалось, к настоящему времени несомненный приоритет во всём мире имеют современные методы, основанные на подходе Бёрда моделирования динамики «ансамбля молекул». Но так было не всегда. Одно время приоритет имели методы статистического моделирования «пробных частиц», основанные на подходе Хэвиленда. Возможно, в будущем появятся его эффективные схемы, как это уже было раньше, когда ещё не было тех эффективных схем подхода Бёрда, о которых речь шла выше. Или новый класс задач, для которых эти схемы станут приоритетными. Но уже сейчас можно выделить некоторые проблемы физической химии, для которых метод пробных частиц оказывается предпочтительнее. Но и, конечно, это класс линейных задач, с которых он, собственно, и начинался [2]. Есть ещё одно явное преимущество этого метода, которое состоит в том, что для него, в отличие от метода Бёрда, так остро проблема соответствия решению кинетического уравнения не стоит. Что касается вычислительной аэродинамики, то он основан на линеаризованном уравнении Больцмана (11).

При разработке схем стационарного статистического моделирования, основанных на методе Хэвиленда - движения «пробных частиц», процесс решения можно рассматривать как решение уравнения Больцмана

где

в следующем интегральном виде

где граничная функция распределения.

Это уравнение, записанное в интегральном виде

представляет собой в каждой k-ой итерации линеаризованное кинетическое уравнение, которое в этой итерации решается методом Монте-Карло, по процедуре Улама-Неймана, описанной выше.

В каждой итерации вычисляется макропараметры, входящие в исходное уравнение (2) и и после этого переходят к следующей итерации. Если метод последовательных приближений сходится, то переход от одной итерации к другой в конечном итоге, приводит к решению кинетического уравнения. Обычно решение математических уравнений и прямого моделирования потоков разреженного газа - традиционная область применения методов Монте-Карло. Мы рассмотрим нетрадиционное применение статистического моделирования для решения задач сплошной среды и турбулентных течений.

6. Метод прямого статистического моделирования для потоков невязкого идеального газа [2]

Потоки газа в широком диапазоне разреженности среды описываются уравнением Больцмана

Посредством схемы "перенос-релаксация" на малом промежутке времени исходное уравнение можно представить в виде двух независимых уравнений:

,

,

которые описывают перенос без столкновений, и пространственно однородную релаксацию (здесь I(f) обозначает интеграл столкновений).

В [2] предлагается моделирование потоков сжимаемого идеального газа посредством локально равновесной функции распределения :

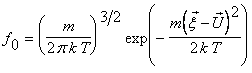
Рассматривалась 1D задача формирования ударной волны. На уровне частиц алгоритм имеет следующую структуру. Ансамбль N частиц со скоростями и внутренними энергиями в интервале времени проходит этапы свободного переноса и однородной релаксации в каждой ячейке. После каждого из этих этапов в ячейках осреднением по частицам определятся макропараметры. В этом случае граничные условия соответствуют зеркальному отражению частиц от поверхности (условие непротекания). Выбор интервала времени основан на условии малого изменения функции распределения в рассматриваемой ячейке:

.

Более определенно,

Где s < 1, скорость звука. Таким образом выбор интервала времени соответствует условиям сплошной среды. Выбор размера ячейки основывается на малых изменениях макропараметров. Вычисление макропараметров совершается следующим образом:

,

.

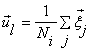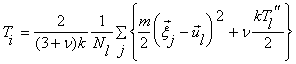Перенос частиц вдоль траекторий в течение времени определяется формулой:

.

Здесь - температура в начальной ячейке, - число частиц в ячейке на данном шаге . После того, как выполнено вычисление макропараметров, на основе функции распределения с новыми макропараметрами необходимо разыграть ансамбль по скоростям , . Предлагается следующий алгоритм моделирования. Молекулярные скорости на шаге случайно разыгрываются в соответствии с функцией :

,

,

.

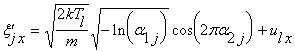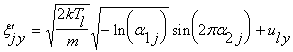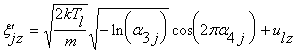
- случайные величины, равномерно распределенные на интервале (0,1). Для простоты обозначений принята 1D нумерация ячеек . Определяется только половина величин , другая - определяется симметрично. Применяется алгоритм для точного сохранения массы, импульса и энергии. Вычисления были выполнены для клина с полууглом раствора 10⁰ и с нулевым углом атаки. Были установлены условия местной однородности потока на верхних и обратных границах сетки. Полученные данные представлены на Рис. 8.

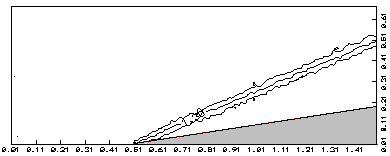
Фиг. 8. Поле плотности.

Данные показывают хорошее согласие с теорией (для a=10⁰ и g= 1,4 угол наклона ударной волны 27,4⁰ . Одна из общих особенностей - то, что ударная волна размазывается на 2-3 ячейки, что является типичным для методов с низким порядком точности. Таким образом структура потока получена правильно. Значения макропараметров находятся в близком соответствии с теоретическими результатами с указанной точностью.

Исследовалась также интересная задача о вычислении поля течения в окрестности плохо обтекаемого тела (сверхзвуковое обтекание торца параллелепипеда при g=1.4, М_¥=3). Используя симметрию потока, рассматривался один квадрант полной области течения. Сетка бралась размерами 60x30x30. Ячейки брались прямоугольной формы. Поток около угловых точек и ребер специально не рассматривался. Вычисления были выполнены подобно случаю клина. Данные расчетов представлены на рис. 9.

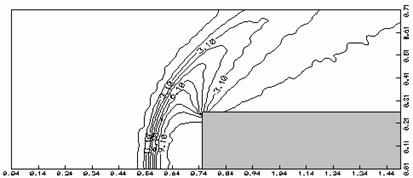
Фиг. 9. Поле давления в плоскости z = 0.

Местоположение отделенной ударной волны может быть оценено, используя имеющиеся расчетные данные в окрестности торца круглого цилиндра. Необходимо отметить, что дозвуковая область существует на конце торца. Метод, оказывается удобным для потоков с различной скоростной структурой (М. < 1 и M>1). Форма ударной волны показана на рис. 5.

Особенности данного метода состоят в том, что структура потока, включая дозвуковые области, описывается верно. Благодаря консервативности метода поверхности разрыва плавно сглаживаются. Для получения основного приближения достаточно небольшого количества частиц и, соответственно, малого времени установления. Для получения результатов с большей точностью должно быть увеличено число частиц грубого приближения в соответствии с оценкой статистической ошибки. Таким образом, статистическая точность 3-5 % может быть получена на небольшом времени. Метод может использоваться для моделирования стационарных и нестационарных течений а также удобен для задач со сложной геометрией и сложными физическими процессами (перенос излучения, испарение, конденсация, горение и т.д.), где применение обычно используемых газодинамических методов усложнено.

Фиг. 10. Форма ударной волны.

7. Описание турбулентных течений. Жидкостная модель описания [16,21]. В качестве обобщения применения кинетических моделей в сплошной среде была сделана попытка описания турбулентных явлений. В частности, исследовался пример диссипации турбулентного пятна. Здесь, как и в динамике разреженного газа, решается проблема на уровне функции распределения. Только теперь аргументом является не молекулярная скорость x, а пульсации скорости жидкой частицы v. Еще Прандтль обратил внимание, что имеется аналогия между разреженным газом и турбулентной жидкостью.

В модели Яницкого каждая частица в ячейке имеет новое качество (см. табл. 1). Жидкая частица, как и прежде, характеризуется физическими координатами и скоростью. Для этой функции распределения предлагается модель кинетического уравнения, аналогичная модельному уравнению в динамике разреженных газов.

Таблица 1 . Описание среды посредством функции распределения

Динамика разреженного газа

Турбулентность

Частицы

Молекулы ri, координаты молекул ci, скорости молекул

Жидкие частицы xi, координаты частиц vi, скорости пульсаций

Функция распределения

Для молекул f=f(t, r, c) , плотность

Для жидких частиц f=f(t, x, v) , нормировка

Моменты

, макроскопическая скорость (c-u), тепловая скорость

, средняя скорость (v-u), флуктуации

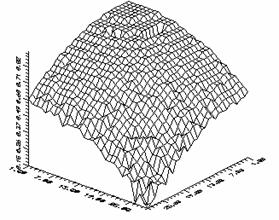
7. Задача о диссипации турбулентного пятна.

Фиг. 11. Диссипация турбулентного пятна (начальная область)

Главная цель рассмотрения состояла в сохранении основных принципов прямого статистического моделирования.

Для описания турбулентности используется кинетическое уравнение Онуфрииева

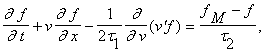
где 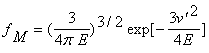- нормальный закон, и E - турбулентная плотность энергии.

Это кинетическое уравнение аналогично модельному уравнению Крука.

Здесь схема моделирования построена согласно тем же самым принципам как в динамике разреженных газов. Рассматриваются жидкие частицы в ячейках и процесс разделяется на три основных шага:

конвективный перенос

;

турбулентная диссипация энергии

и перераспределение энергии

.

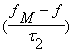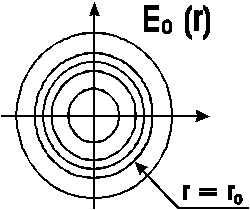
Численно решалась задача о диссипации пятна, чья энергия первоначально сконцентрирована в области с характерным радиусом r₀, рис. 6, характерный радиус пятна и плотности турбулентной энергии E_m (t) в центре пятна. Начальные данные:

,

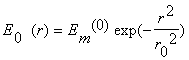f (0, r, v) = f₀ (z, v)

.

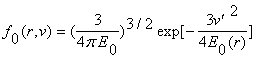Сравнение с экспериментальными данными приведено на рис. 7 ( , ).

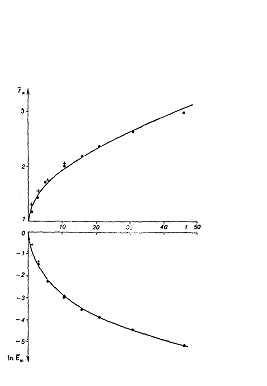
Фиг.12. Диссипация турбулентного пятна.

---- данные эксперимента (Naudasher), + прямое моделирование)

Кинетические модели турбулентности более информативны, так как они описывают пульсации на уровне функции распределения. Подобный подход к описанию турбулентности представляется перспективным, поскольку позволяет учитывать крупномасштабные турбулентные процессы непосредственно от схем уравнений переноса, а мелкомасштабные пульсации с помощью прямого статистического моделирования.

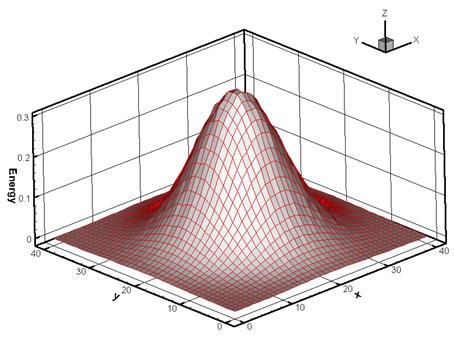
Фмг. 13 Распределение удельной энергии в турбулентном пятне t=0

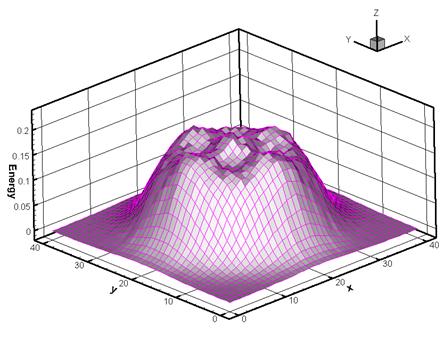
Фиг. 14 Распределение удельной энергии t=40

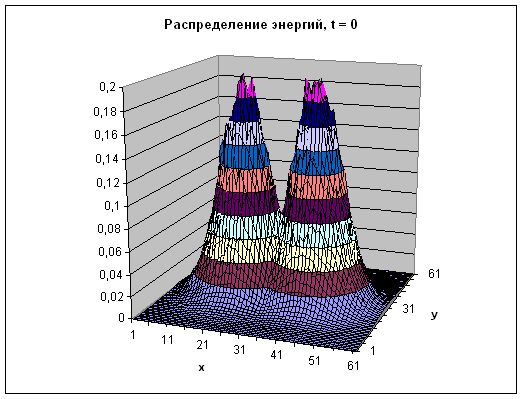
Фиг. 15 Функции распределения турбуленой энергии взаимодействующих пятен

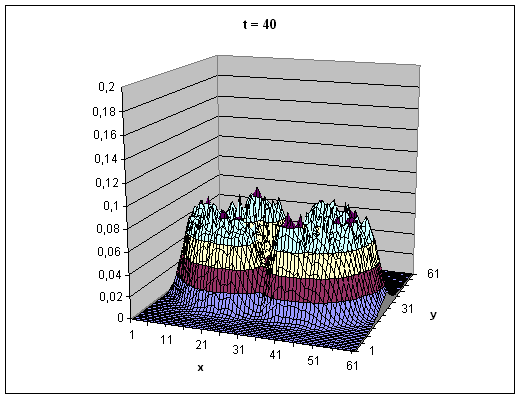
Фиг. 16 Функции распределения турбуленой энергии взаимодействующих пятен

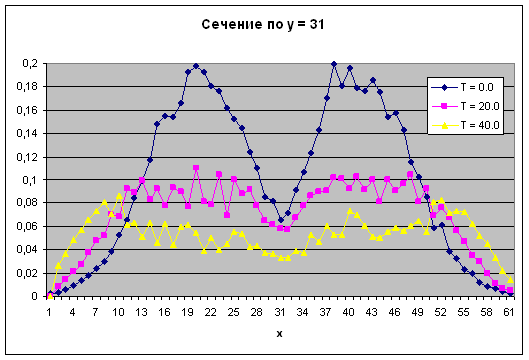
Фиг. 17 Взаимодействие двух тубулентных пятен (распределение энергий)

8. Описание турбулентности с помощью модели трехволнового резонанса [24]. Рассмотрим уравнения Рейнольдса для средних величин U и V и пульсаций u, v, w, p в приближении пограничного слоя. Пусть d - характерный поперечный масштаб потока, L - продольный масштаб. Поскольку при оценке величин в исходных уравнениях сравниваются силовые характеристики, , - толщина потери импульса. Таким образом . Практически . Обозначим

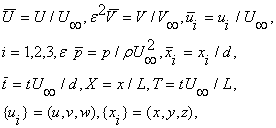
Тогда уравнения для , будут иметь вид:

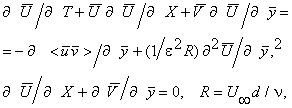
И для

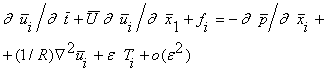
В этих уравнениях введены: {} = (), В качестве граничных условий для этих уравнений примем: Предполагается, что R>>1, R>>1.

Преобразуя систему к уравнениям для вертикальных компонентов скорости и завихренности при предположении отсутствия резонанса волн Толмина-Шлихтинга (T-S) с волнами Сквайра, уравнение для вертикальной компоненты завихренности далее ради простоты будет опущено. Если разложить вертикальную компоненту скорости по низшему дискретному спектру волн Толмина-Шлихтинга, получим

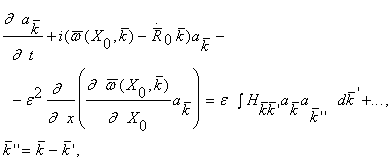
где , , являются соответственно безразмерным волновым вектором, собственными числами уравнения Орра-Зоммерфельда (O-S), - "центр масс" координат волнового пакета. Амплитуды связанны с вертикальными скоростями возмущения v(x, y, z) следующим образом

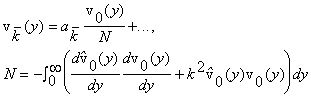
где - низшая T-S мода, - собственная функция, - Фурье-образ v(x, y, z).

При соответствующих предположениях в этом случае для "плотности" волновых пакетов I(k) = <> / получается уравнение переноса:

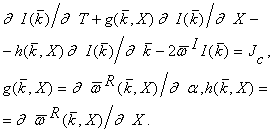
Это уравнение напоминает кинетическое и описывает рождение квазичастиц в области неустойчивости низшей моды T-S волн, их перемещение с групповой скоростью g(k, X) под действием "силы" (-h (k, X)), и также распад и слияние частиц, обусловленные трехволновым резонансом, который описан членом . В элементарном случае интеграл столкновений такого типа имеет вид:

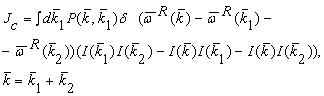
Для исследования уравнения для волнового пакета , аналогичного кинетическому, в принципе, может быть применен метод прямого статистического моделирования, хорошо зарекомендовавший себя при моделировании явлений, описываемых кинетическими уравнениями.

Например, можно предложить следующую методику прямого статистического моделирования (Монте-Карло). Будем искать решение уравнения для за время , считая, что - мало. Можно написать решение уравнения для через интервал времени следующим образом:

Будем трактовать функцию как плотность некоторых частиц в пространстве векторов . Эта плотность с течением времени меняется, и связь этой плотности в момент времени с плотностью в момент времени дается предыдущим уравнением.

Поскольку считается, что в момент времени известна, то величины , и известны тоже. Если выбрать таким, чтобы , то можно воспользоваться принципом суперпозиции. То есть плотность с вероятностью в момент времени равна , а с вероятностью равна . Если моделировать эту плотность в момент времени t некоторым количеством частиц (в начальный момент времени это количество частиц может равняться нулю), то с вероятностью эти частицы не меняют своих координат, а с вероятностью либо рождаются новые частицы с частотой , либо координаты у частиц меняются с частотой . Выражение, связанное с рождением частиц можно рассматривать как суперпозицию.

,

Алгоритм вычисления выглядит следующим образом:

1. В пространстве векторов задаются координаты некоторого количества частиц в соответствии с начальной плотностью (которая, быть может, равна нулю, и в этом случае в пространстве частиц нет)

2. Вычисляются , , . В том случае, если окажется, что , изменяется .

3. С вероятностью поле не меняется, и после вычисления соответствующих макровеличин осуществляется переход на следующий шаг (п. 2).

4. С вероятностью происходит рождение частиц.

4.1. С вероятностью частицы рождаются с плотностью .

4.2. С вероятностью частицы в поле меняют свои координаты.

4.3. Достигнув границы расчетной области, частицы исчезают.

После вычисления соответствующих макровеличин осуществляется переход на следующий шаг.

9. Моделирование эволюции вихревой системы в разреженном газе[25].

Рассматривается уравнение Больцмана:

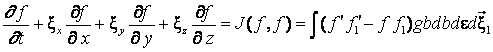
где , , , , скорости , , , соответствуют частицам до и после столкновения,

– относительная скорость, b – прицельное расстояние, e – азимутальный угол.

Метод расщепления:

– релаксация

– перелет

Начальные условия

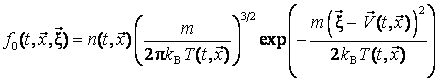
где n – концентрация частиц, T – температура,   –  вектор скорости частицы, m  –  масса частицы, k_B – постоянная Больцмана.

Используется схема «Белоцерковского-Яницкого», приспособленный для решения нестационарных задач и модель твердых сфер для моделирования столкновений.

9.1.Проверка алгоритма проводилась на одномерной задаче о распаде разрыва

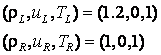
На границах реализуется зеркальное отражение частиц.

Режимы: Kn®0, Kn®¥, Kn=0.01, Kn=0.005, Kn=0.0025

Сравнение проводилось с теоретическими результатами и расчетами на основе конечно-разностных методов

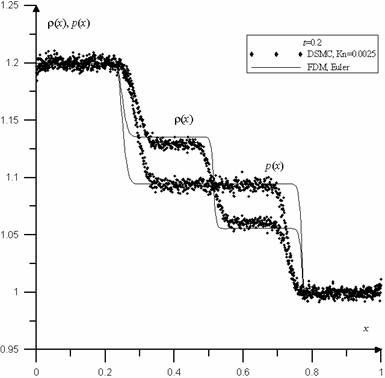
Рис. 18. Распределение плотности и давления для момента времени t = 0.2

в задаче о распаде разрыва при Kn = 0.0025.

9.2. Постановка задачи Тейлора–Грина

Начальные и граничные условия

,

,

,

,

0<x<1, 0<y<1

A = 0.5, B = –0.4, C = D = 0.1

F(x+1, y+1) = F(x, y).

Mmax = 0.39 – число Маха, определенное по начальному полю,

g = 5/3 – показатель адиабаты в одноатомном газе,

Kn = 0.01 – число Кнудсена,

Re = Mmax/Kn = 39 – число Рейнольдса.

Используется сетка 110×110×1

На границах реализуется периодический перенос частиц в задаче об эволюции вихревой системы.

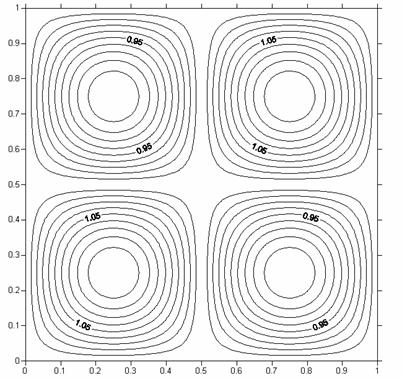
Рис. 19. Пространственное распределение плотности при t = 0

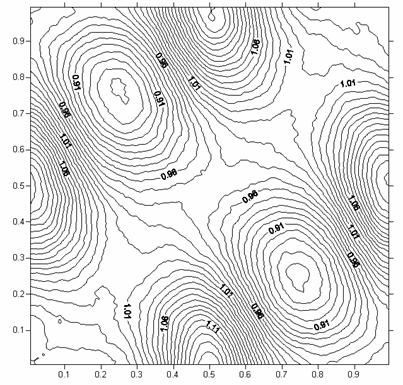
Рис. 20. Пространственное распределение плотности при t = 0.1

в задаче об эволюции вихревой системы.

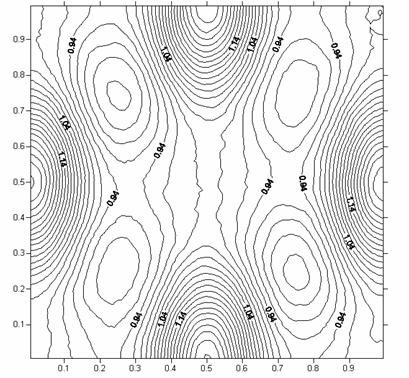
Рис. 21. Пространственное распределение плотности при t = 0.2

в задаче об эволюции вихревой системы.

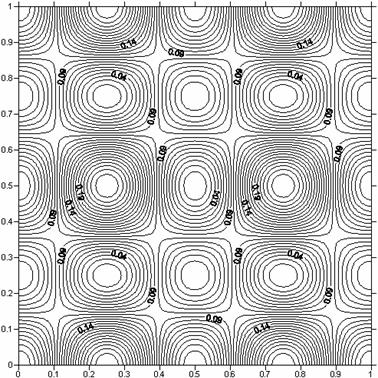
Рис.22. Пространственное распределение энергии при t = 0

в задаче о эволюции вихревой системы.

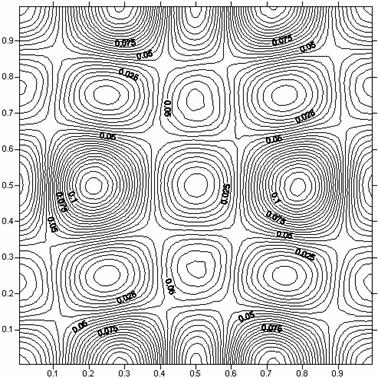
Рис.23. Пространственное распределение энергии при t = 0.1

в задаче о эволюции вихревой системы.

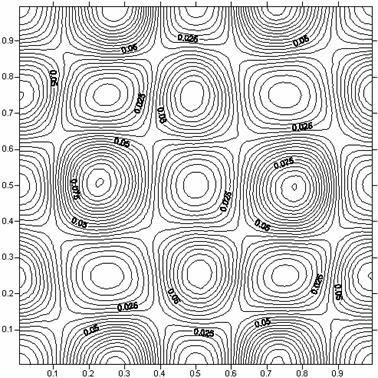
Рис.24. Пространственное распределение энергии при t = 0.2

в задаче о эволюции вихревой системы.

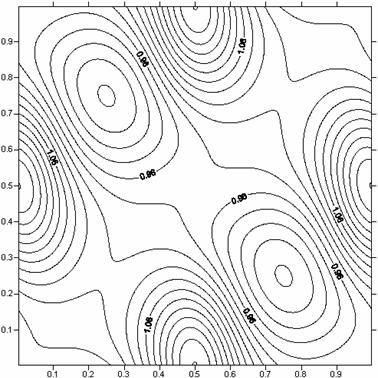
Рис. 25. Пространственное распределение плотности при t = 0.1

в задаче о эволюции вихревой системы Euler.

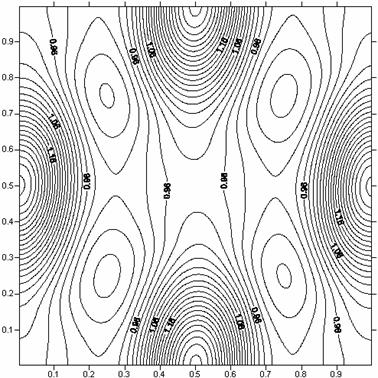
Рис. 26. Пространственное распределение плотности при t = 0.2

в задаче о эволюции вихревой системы Euler.

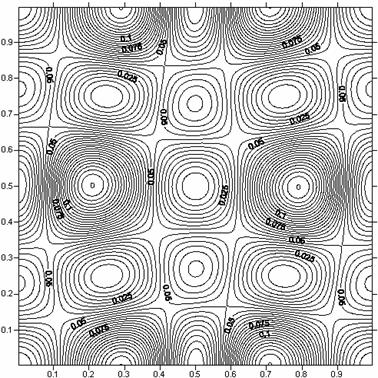
Рис. 27. Пространственное распределение энергии при t = 0.1

в задаче о эволюции вихревой системы Euler.

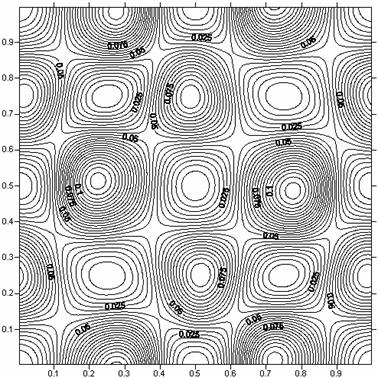
Рис. 28. Пространственное распределение энергии при t = 0.2

в задаче о эволюции вихревой системы Euler.

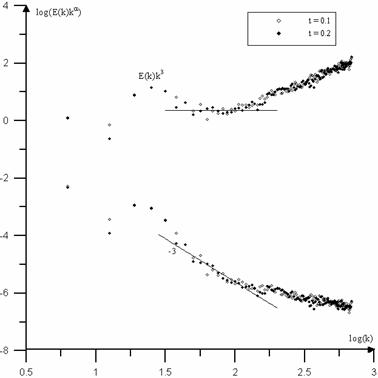
Рис. 29. Спектр энергии при t = 0.1 и 0.2

в задаче о эволюции вихревой системы.

Эта работа поддержана Российским Фондом Фундаментальных Исследований, Грант №04-07-90345, а так же Государственной Программой Поддержки Ведущих Научных Школ, Грант №96-15-96063.

Литература

1. Hall A. On an experiment determination of . Messeng. Math. № 2, 1873

2. Metropolis N., Ulam S. The Monte-Carlo method. J. Amer. Stat. Assos. 44, № 247, 1949

3. Владимиров В.С., Соболь И.М. Расчёт наименьшего характеристического числа уравнения Пайерлса методом Монте-Карло. Вычислит. математика, №3, 1958

4. Haviland J.K. Lavin M.D. Application of the Monte-Karlo Method to Heat Hauster in Rarefied of Gases. Phis. Fluids,. v.s, N 11. 1962

5. Bird G.A. Shock-Wave Structure in rigid Sphere Gas. In Rarefied Gas Dynamics, vol.1. N.-Y., Acad. Press, 1965

6. Ермаков С.М. Метод Монте-Карло и смежные вопросы. М. Наука, 1985

7. Кац М., Вероятность и смежные вопросы в физике. М., Мир, 1965

8. Bhathnagor P.D., Gross E.P., Krook M.A. A model for collision processes in gases. Phis.rev, 94. 1954 9. Шахов Е.Н. Поперечное обтекание пластины разреженным газом. Изв. АН, МЖГ, N6, 1972.

10. Яницкий В.Е. Статистическая модель течения идеального газа и некоторые её особенности. В кн. Числ. Методы механ.сплошной среды. Новосибирск, СО АН СССР, т. 6, №4, 1975

11. Белоцерковский О.М., Яницкий В.Е. Статистический метод “частиц в ячейках” для решения задач динамики разреженного газа 1, П. ЖВМ и МФ, т.15, N5, 1975

12. Белоцерковский О.М. Вычислительный эксперимент: прямое численное моделирование сложных течений газоводинамики на основе уравнений Эйлера, Навье-Стокса и Больцмана. «Кармановская лекция», Ин-т динамики жидкости им. Кармана, Брюссель, 1976

13. Белоцерковский О.М., Яницкий В.Е. Численные методы в динамике разреженных газов. В кн. Труды IV Всесоюзной конференции по динамике разреженного газа и молекулярной газовой динамике. М. Издательский отдел ЦАГИ, 1977

14. Белоцерковский О.М., Яницкий В.Е. Прямое численное моделирование течений разреженного газа. В сб. Числен. мет. в дин. разреж. газов. АН СССР, ВЦ, М, вып.3, 1977

15. Белоцерковский О.М., Яницкий В.Е. Проблемы численного моделирования течений разреженного газа. Успехи механ., т.1, вып.1\2? 1978

16. Белоцерковский О.М. Численное моделирование в механике сплошных сред.- М: Наука, 1984

17. Ерофеев А.И., Перепухов В.А. Расчет поперечного обтекания пластины потоком разреженного газа. Изв. АН СССР, МЖГ, N4, 1976

18. Горелов С.Л., Ерофеев А.И. Влияние внутренних степеней свободы на обтекание пластины гиперзвуковым потоком разреженного газа. Изв. АН СССР, МЖГ, МЖГ, N6, 1978

19. Белоцерковский О.М., Ерофеев А.И., Яницкий В.Е. О нестационарном методе прямого статистического моделирования течени1 разреженного газа. ЖВМ и МФ, т.20, № 4, 1980

20. Белоцерковский О.М., Ерофеев А.И., Яницкий В.Е. Прямое статистическое моделирование задач аэродинамики. ВЦ АН СССР, М. 1983

21. Belotserkovskiy O.M., Yarofeev A.I., YanitskiyV.E. Direct Monte-Carlo simulation of aerogydrodynamics problems // Proc. 13^th Internat. RGD Symp. New York: Plenum Press, 1985. V. 1. P. 313-332.

22. Хлопков Ю.И. Решение линеаризованного уравнения Больцмана. ЖВМ и МФ, N5, 1973

23.. Khlopkov Yu. I,. Kravchuk A. S. Simulation of Rarefied Gas Flow and of a Continuum. XVII Inter. Symp. on RGD, V.1, Aachen, 1990

24. Gorelov S. L., Zharov V. A., Khlopkov Yu. I. The Kinetic Approaches to the Turbulence Description. Proceedings of the 20^th International Symposium on Rarefied Gas Dynamics, Beijing, China, 1997.

25. Хлопков Ю.И., Воронич И.В., Ровенская О.И. Прямое статистическое моделирование эволюции вихревой системы в разреженном газе. Труды Международной конфереренции «Авиадвигатели XXI века», издательсво ЦИАМ, 2005