крупномасштабные динамические структуры

 в турбулентном пограничном слое

 

Хлопков Ю.И., Жаров В.А., Горелов

 

Московский физико-технический институт

Ул. Гагарина 16, г. Жуковский Московской обл., 140180 Россия

khlopkov@falt. ru

 

1.История вопроса. В настоящее время получено колоссальное количество данных о динамике турбулентного движения несжимаемой жидкости в пограничном слое на пластине, в которых обнаружены структурные элементы взаимодействия обтекаемой поверхности с потоком. Экспериментальные данные получены разными исследователями разными методами и выявляют некоторые общие черты этого взаимодействия. Настало время глубокого теоретического осмысления этих результатов и построения на их основе глобальных теорий турбулентного движении. Ниже очень сжато перечисляются основные результаты экспериментальных исследований, которые можно, на наш взгляд, взять на вооружение при построении математических моделей.

Разложение нестационарного движения было впервые предложено О. Рейнольдсом в 1894 году [1]. Величины, описывающие течение, разделялись на среднюю и флуктуирующую части, и после подстановки в уравнение Навье-Стокса в результате получалась система уравнений, идентичная по форме исходной системе, за исключением членов конвективных напряжений, которые возникают из осредненных произведений флуктуаций скорости. Для того чтобы замкнуть систему уравнений, необходимо иметь еще соотношение между конвективными напряжениями и полем средней скорости. До недавнего времени многие теоретические и экспериментальные исследования были сосредоточены на поиске связей, которые были бы применимы ко все большему многообразию средних течений с надеждой найти универсальное соотношение для “турбулентной жидкости”. Надежда на универсальную модель турбулентности была постепенно заменена растущей уверенностью в том, что формулировка адекватной теории требует значительно лучшего понимания физики турбулентного течения.

Для исследователя 1920-1930 годов турбулентность была существенно стохастическим явлением, имеющим хорошо определенное и воспроизводимое среднее, на которое было наложено стохастически флуктуирующее поле скорости. Движение характеризовалось широкой областью масштабов, лимитированных только полными размерами течения. Эта картина стохастически взаимодействующих элементов течения разных масштабов привела к появлению полуэмпирических теорий Прандтля [2] и Тейлора [3], в которых конвективные напряжения были связаны со средним потоком с помощью эффективной вихревой вязкости (введенной Бусинеском в (1877 году [4])  или длины смешения.

         Рассмотрение эволюции спектра однородной и изотропной турбулентности привело к важному наблюдению, что энергосодержащие структуры  изотропной турбулентности не зависят непосредственно от величины вязкости жидкости. Оказалось, что при достаточно больших числах Рейнольдса, когда жидкость заведомо турбулентна, энергосодержащие структуры подобны для всех значений чисел Ренольдса. В дополнение к этому также было отмечено, что если число Рейнольдса достаточно велико, зона диссипации и зона генерации турбулентной энергии сильно разделены в пространстве волновых чисел. В этом случае мелкомасштабное движение находится в состоянии локального изотропного равновесия.        

Новый элемент был добавлен к физической картине турбулентности Корзиным [5] и Таунсендом [6], которые показали, что внешние границы турбулентных сдвиговых течений, особенно в струях и следах, находятся только в состоянии перемежаемой турбулентности. В середине 50-х годов физические представления успешно развились до состояния, которое можно охарактеризовать следующей картиной (Таунсенд [8]), связывающей ламинарный подслой Корзина и Кистлера [7] с полем турбулентной жидкости почти однородной интенсивности. Динамические характеристики этого поля подобны характеристикам изотропной турбулентности. Турбулентная жидкость приводится в движение медленным конвективным сносом совокупности больших вихрей, чьи размеры сравнимы с шириной потока и много больше, чем масштаб вихрей, содержащих большую часть турбулентной энергии.

 

..

 

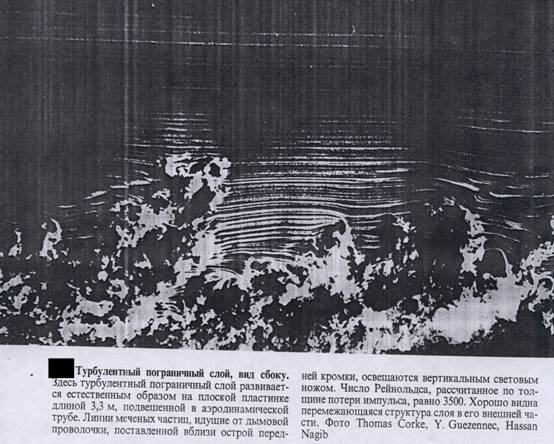Рис.1. Пограничный слой на плоской пластине (из альбома M. Van Dyke[31]).

 

 

 Во внешней по отношению к турбулентной поверхности раздела области течения движение нестационарно. В этой области незавихренное потенциальное течение индуцировано движением жидкости около границы.

         Таунсенд рассматривал большие вихри и мелкомасштабную турбулентность как главную черту двойной структуры и подчеркивал важность больших вихрей в процессе переноса. Он также подчеркивал, что большие вихри должны принимать квазидетерминистическую форму, и пытался нарисовать картину крупномасштабного вихревого движения достаточно реалистичную для того времени. Попытка создать такую картину обычно принимала форму заключений, основанных на осреднении по большим интервалам времени пространственного корреляционного тензора (Фавр)[35]

 

  ,

измеренного в эйлеровой системе отсчета. Обширные корреляционные измерения (Grant H.Z., Rayne F.R., Lamley J.L, Townsend A.A. )

 [9-12] в различных турбулентных течениях выявили ряд характерных образований, которые можно было интерпретировать как когерентные вихревые структуры.

          В начале 60-х годов были выполнены эксперименты, которые начали изменять взгляды на турбулентность. В последние двадцать лет исследований в отношении турбулентности появилась уверенность, что характеристики переноса импульса, энергии и т.п. турбулентных сдвиговых течений определены крупномасштабным вихревым движением детерминированным, а не случайным. Форма, интенсивность и масштаб этих организованных движений изменяется от потока к потоку, и вместе с ними изменяются методы их определения.

 

2. Структура осредненного течения. Самые ранние наблюдения организованного движения были сделаны в турбулентном пограничном слое (ТПС), текущем вдоль стенки, где течение наиболее сложно. Это связано с тем, что это  - течение, которому всегда уделялось огромное внимание из-за его технической важности, и было крайне желательно выявить его структуру в первую очередь (Рис.2).

                                                           

Рис.2. Подслой турбулентного пограничного слоя

 

 

Средний профиль скорости в турбулентном пограничном слое (Рис.1, Рис.2 и Рис.3) может быть разбит на три части (Кадер Б.Л., Яглом А.М.) [13]):

 

 

 

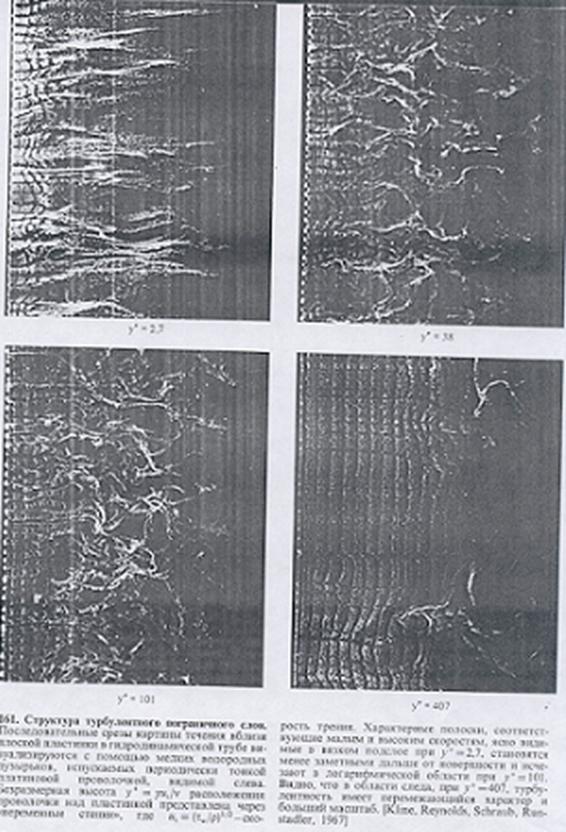
Рис.3. Структура турбулентного пограничного слоя. Бёрстинг.

 

 

           Вязкий подслой:  

           Буферный подслой .

           Логарифмический и внешний слои .

Имеется несколько эмпирических формул для среднего компонента продольной скорости (Cantwell B.J.)[30] u+(y+,y/d), d  - толщина пограничного слоя, которые выражаются через набор переменных

 

 

 

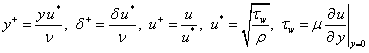
          Первое замечательное свойство турбулентного пограничного слоя – это универсальность пристеночного поведения. Независимо от величины градиента давления, от шероховатости стенки или от числа Рейнольдса наблюдается логарифмическая зависимость скорости от координаты Кроме того, суммирование скорости генерации турбулентной энергии по всей толщине пограничного слоя приводит к результату, что первые 5% пограничного слоя вносят больше половины генерируемой турбулентной энергии. Этот результат был первым толчком для ранних работ и остается таковым для большей части работ по структуре турбулентного пограничного слоя, выполненных сегодня.

          Отметим, что в работе (Barenblatt G.I., Chorin A.J., Prostokishin V.M.)[15] рассматривается возможность другой структуры турбулентного пограничного слоя (степенное поведение вблизи стенки), которая переходит в описанную выше только при стремлении числа Рейнольдса к бесконечности.

 

4. Внутренняя область. Начиная с конца 50-х годов, в Стенфорде начались серии экспериментов с использованием визуализации течения для исследования турбулентного пограничного слоя. Эти усилия сконцентрировались в работе Клайна и др.( Kline J., Reynolds W.C., Schraub F.A., Runstadler P.W.) [14].  Выявилось несколько новых свойств течения в пристеночной области ТПС.

          В эксперименте наблюдалось взаимодействие стриков, высоко- и низкоскоростных областей придонного течения, с внешними частями течения посредством последовательности из четырех событий: медленное поднятие, подъем, внезапные осцилляции и распад. Последовательность, состоящую из трех событий, от подъема до распада, они назвали “берстингом” (Рис.2, Рис.3 и Рис.4).

 

                                                                                    

 

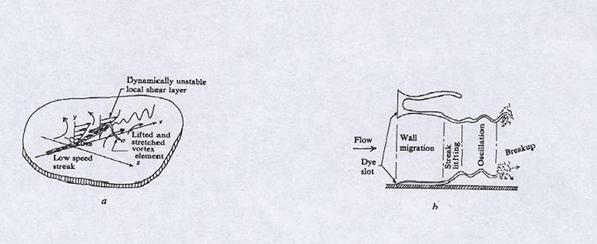
Рис.4. Схематическое представление нестационарной структуры  турбулентного пограничного слоя. (a) Механика распада стрика Kline J., Reynolds W.C., Schraub F.A., Runstadler P.W [14], (b) Последовательность событий в (a).       

 

 

 

          В дополнение к этому они обнаружили, что благоприятный градиент давления  стремится уменьшить частоту берстинга, а неблагоприятный – увеличить. Было подтверждено, что берстинг играет решающую роль в генерации турбулентной энергии, что он преобладает в процессах переноса между внутренними и внешними областями пограничного слоя и, таким образом, играет важную роль в определении структуры всего слоя. Клайн Reynolds W.C., Schraub F.A., Runstadler P.W и др. [14] оказались способными оценить пространственные масштабы движения, связанного со стриками и берстами. Из данных визуальных наблюдений они получили, что среднее поперечное расстояние между стриками (т.е. расстояние, равное одной длине волны) для гладкой поверхности при произвольном градиенте давления было равно приблизительно  (Рис.2., Рис.3., Рис5).

.

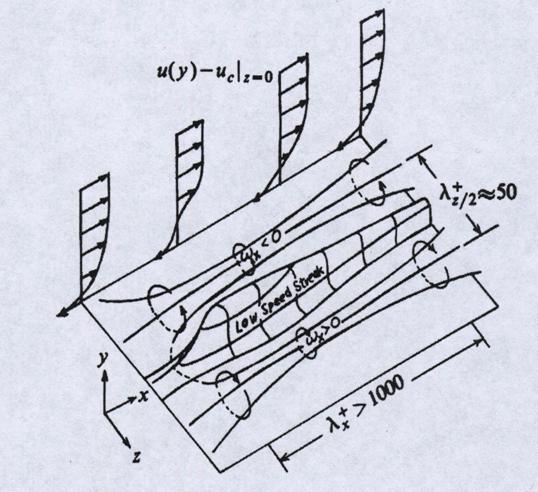
Рис.5.

          Собранные вместе, эти начальные наблюдения вызвали дальнейшие работы по турбулентному пограничному слою, которые показали важную связь между квазидетерминистическими, повторяющимися нестационарными движениями жидкости, генерацией турбулентности и поддержанием среднего турбулентного потока.

          Рао и др. (Rao K.N., Narasimha R., Narayanan M.A.B.) [16] после проверки данных в очень широком диапазоне чисел Рейнольдса  показали, что даже в пристеночном слое средний период берста выражается через внешние переменные , со средним временем между берстами, равным

 

 

Более того, они обнаружили, что средняя частота берстов не изменялась существенно с изменением расстояния до стенки. Авторы предположили также смешанный вариант обезразмеривания к внутренним переменным для поперечных пространственных масштабов и к внешним – для времени между берстами, который приводит к параметру  (где  - толщина вытеснения,  - частота берста на единицу размаха) как к величине, практически не зависящей от числа Рейнольдса.

         В работе (Grass A.J.) [17] обнаружено, что эжекция и всплески наблюдались независимо от поверхностной шероховатости. Пристеночное течение в пограничном слое над полностью шероховатой поверхностью должно сильно отличаться от течения над гладкой поврехностью. Но, как видно, основная структура организованного движения существенно неизменна. Аналогичные данные, по большей части косвенные, имеются и в отношении поверхностей со слабым вдувом  – отсосом (см., например, (Вигдорович И.И.)[28]), поверхностей волнистых или колеблющихся в поперечном направлении.

Блэквельдер и Экельманн [18] проделали достаточно подробное исследование структуры пристеночных стриков для подтверждения наличия продольной и поперечной завихренности у стенки (Рис.5). Они нашли, что интенсивность продольных вихрей на порядок меньше, чем средняя поперечная завихренность. Они выделили низкоскоростной стрик, который наблюдался Клайном и др. как область накопления между продольными вихрями, где вертикальная компонента вторичного движения направлена от стенки, кроме того, они нашли длину продольных вихрей равной .

 

4. Внешняя область. (В качестве общего правила принята терминология, согласно которой “пристеночный слой” относится к  и включает в себя вязкий подслой и часть логарифмической), Внешняя область – все остальное.

 Коважный и др. ( Kovasnay L.S.G., Kibens V., Blackwelder R.F.,) [19] использовали условно осредненные автокорреляционные функции нескольких переменных, описывающих течение, для того, чтобы нарисовать трехмерную карту внешней структуры (Рис.6).

 

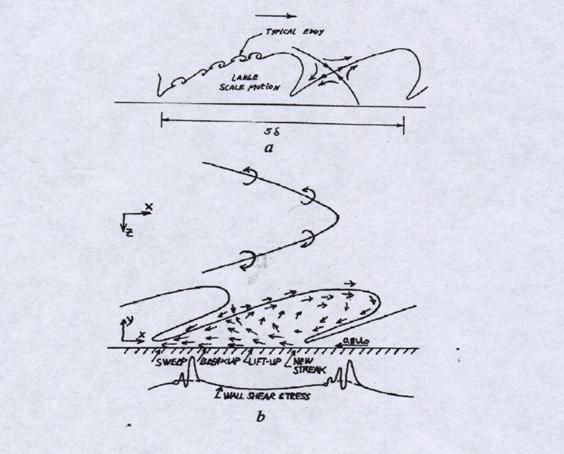
Рис.6. Модель внешней структуры турбулентного пограничного .слоя [19-21]

(Kovasnay L.S.G., Kibens V., Blackwelder R.F., Falco R.E. Blackwelder R.F.).

 

 

Они обнаружили, что завихреность разрывна при переходе через границу, отделяющую турбулентные неоднородности от внешнего потока, в то время как скорость непрерывна. В дополнение к этому они заметили, что между передней и задней частями турбулентных образований существует большая разница во внешнем потоке. Они подтвердили, что если поток рассматривать в системе отсчета, движущейся со средней скоростью конвекции границы раздела, то жидкость движется в направлении точки торможения, расположенной сзади неоднородности на расстоянии приблизительно . Этот результат получен и в последних исследованиях, посвященных организованным структурам в турбулентном потоке, т.е. задняя часть турбулентного образования наиболее активна, и эта активность связана с седловой точкой в движущейся системе отсчета.

1.         Браун и Томас [22] связали сдвиг на стенке со скоростью поперек слоя. В этой работе показано, что пристеночный сдвиг скорости имел медленно меняющуюся часть и высокочастотную часть, и что обе части были связаны. При этом определена линия максимальной корреляции, которая лежит под углом 18о к стенке в продольном направлении, и сделано предположение, что это является следствием наклона организованной структуры к стенке под острым углом и создания характерного возмущения напряжения на стенке при движении организованной структуры вдоль  пластины со скоростью 0.8U¥. На задней части поверхности раздела внешней структуры был обнаружен резкий скачок скорости. Фалько [20] совместил визуальные и термоанемометрические измерения во внешней части поверхности раздела внешней структуры, которая была связана с движением, созданным за счет генерации напряжений Рейнольдса мелкомасштабными вихрями во внешней области с характерным масштабом . В работах [20, 21] Falco R.E. Coherent motions in the outer region of turbulent boundary layers // Phys. Fluids. 1977. V.20. N 10. P.5124-5132.

Blackwelder R.F., Kovasznay L.S.G. Time scale and correlation in a turbulent boundary layer // Phys. Fluids. 1972. V.15. P. 1545-1554.

 нарисована очень похожая схема организованной структуры.

         Хид и Бандиопадхай [23] использовали визуализацию потока и термоанемометрические измерения, чтобы нарисовать совершенно другую картину. Авторы предположили, что для значений  наиболее характерной чертой пограничного слоя является существование не крупномасштабного когерентного движения, а структур, образованных с помощью случайного слияния элементов течения, имеющих малый размер в продольном направлении, но сильно вытянутых вдоль линий, наклоненных под углом 40о к поверхности (Рис.7).

 

 

 

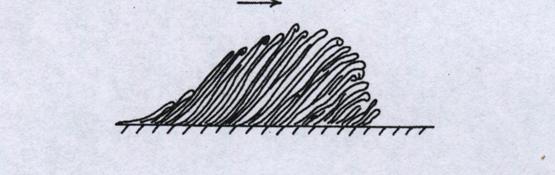
Рис.7 Хид и Бандиопадхай

 

2.     6. Определение когерентной структуры. В соответствии с имеющимися экспериментальными данными можно дать следующее определение [25]: Perry A.E., Lim T.T., Chong M.S., Teh E.W. The fabric of turbulence // AIAA Paper. 1980. N 80-1358.

 когерентная структура определяется как связанная, крупномасштабная турбулентная, жидкая масса с завихренностью, скоррелированной по фазе во всей области пространства, занимаемого структурой, т.е. скрытые трехмерные случайные вихревые флуктуации, характеризующие турбулентность, являются организованной компонентой завихренности, которая скоррелирована по фазе (т.е. когерентна) во всей области расположения структуры. Наибольший пространственный размер, на котором существует когерентная завихренность, есть размер когерентной структуры. Таким образом, турбулентность состоит из когерентных и случайных движений; последние накладываются на первые и обычно простираются далеко за границы когерентной структуры.

 

7. Тройное разложение. В присутствии когерентной можно рассматривать мгновенное поле течения, состоящее из суммы трех компонент (Blackwelder) [25]: независящая от времени компонента, когерентная компонента и некогерентная турбулентность. Т.е. для любых мгновенных переменных

 

 

где ,  - среднее по времени от , fc -среднее по фазе, fr – случайная составляющая. Таким образом в произвольной данной точке, при условии, что фаза структуры тоже известна, могут быть определены три поля.

        

7. Заключение. Перечисленные результаты не оставляют сомнений в существовании когерентных динамических образований, с помощью которых осуществляется генерация завихренности с границы поверхности в поток.

         Тем не менее, в этой совокупности экспериментальных данных есть белые пятна. Например, нет определенности в вопросе о том, какие процессы создают основную часть касательных напряжений на стенке. Часть экспериментальных данных показывает, что это  - результат единичного бёрстинга. В других экспериментах генерация касательных напряжений на стенке связывается с большими градиентами в основании характеристического вихря, который возникает в результате множественного действия берстинговых событий. В этой связи надо отметить также, что есть неопределенность и в определении понятия частоты берстинга, так как можно определять частоту этого явления с помощью единичного датчика, но можно определить частоту берстинговых событий, приходящихся на единицу длины гребенки датчиков. (В обзорной монографии (Хлопков Ю.И., Жаров В.А., Горелов С.Л.)[29] приведено более подробное описание этих и многих других явлений, происходящих в ТПС.)

         Все же, на наш взгляд, приведенных результатов достаточно, чтобы на их основе  попытаться сформулировать математические модели, описывающие процесс генерации завихренности с твердой поверхности обтекаемого тела. Ранее, в рамках вихрепотенциальных течений, были сформулированы “статические” модели динамических структур, принимавших во внимание наличие продольных вихрей (Садовский В.С., Синицина Н.П., Таганов Г.И.) [27] (Рис. 8) и двойную структуру совокупности шпилькообразных вихрей [(Perry A.E., Lim T.T., Chong M.S., Teh E.W.) 24] (Рис.9), с помощью которых удалось очень точно описать профиль средней продольной скорости.

 

.

 

 

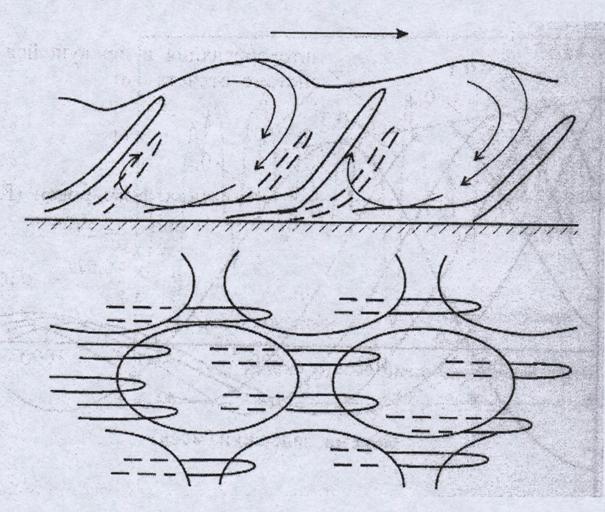
Рис.8. Турбулентный пограничный слой по Фидлеру [32].

 

 

 

 

 

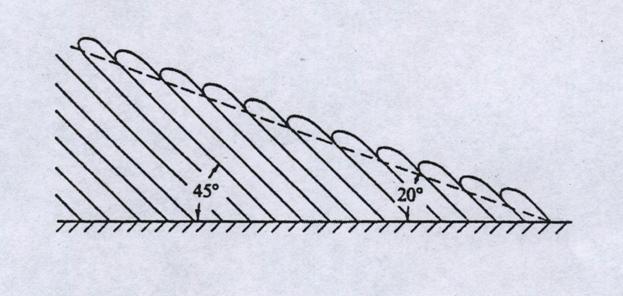
Рис.9. Двойная структура

 

с помощью которых удалось очень точно описать профиль средней продольной скорости. (Tadashi Utami, Totsuo Ueno. [33] (Рис.10.) приводятся значительно более тонкие детали вихревой структуры).

  Тем не менее, современная техника требует дальнейших обобщений данных экспериментов и, в частности, создания нестационарных моделей динамических структур, описывающих вихреволновые процессы в ТПС (Рис.11. Acarlar M.S., Smith C.R.[34]).

 

 

 

 

 

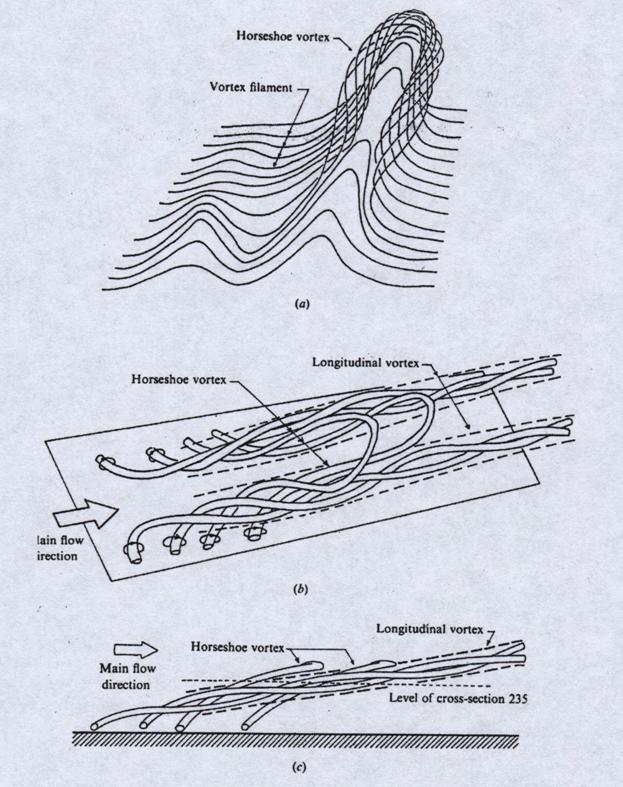
Рис.10. Одна из последних схематических моделей вихревой структуры [33] Tadashi Utami, Totsuo Ueno.

 

  

 

 

 

 

 

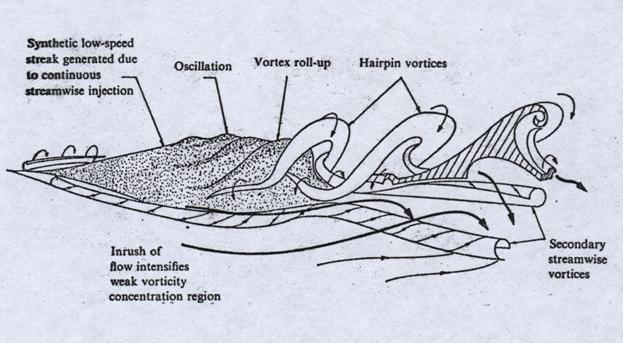
Рис.11. Схематическое представление нестационарного распада низкоскоростого стрика с образованием шпилькообразных вихрей [34] Fiedler H.E. Coherent structure. Advances in turbulence. Proc. of First European Turbulence Conference. Ed. G. Comte-Belo, J. Mathien. Lion, France, 1986.

 

 В этом направлении делаются некоторые усилия (см., например, работу  [26], в которой предложен алгоритм явного выделения когерентных структур в рамках тройного разложения поля скорости).

Авторы надеются, что приведенные экспериментальные данные позволят сформулировать и другие содержательные модели, которые в полной мере выявят возможности управления описанными выше явлениями.

Работа поддержана Российским фондом фундаментальных исследований (02-01-00598), а также программой «Государственной поддержки ведущих научных школ» (НШ-1984-2002.1).

 

Литература

 

3.     Reynolds O. On the dynamical theory of incompressible viscous fluids and the determination of the criterion// Philos. Trans. Roi. Soc. London  Ser. A 1894. V. 186. P. 123-161.

4.     Prandtle L. Bericht uber undersuchungen zur ausgebildeten turbulent // Z. Angew. Math. Mech. 1925. V.5. P. 136-139.

5.     Taylor G.I. Note on the distribution of turbulent velocities in a fluid near a solid wall // Proc. Roy. Soc. London SerA. 1932.  V. 135. P.678-684.

6.     Boussinesq J. Theorie de l’eculment // Mem. Press. Acad. Sci. 1877. V.23. P.16.

7.     Corrsin S. Investigation of flow in axially symmetric heated jet of air: Report /NACA 1943. N 3123.

8.     Townsend A.A. Mesurements in the turbulent wake of a cylinder // Proc. Roy. Soc. London Ser.A. 1947.  V. 190. P.551-561.

9.     Corrsin S., Kistler A. The free boundaries of turbulent flows: Tech. Note / NACA. 1955. N 3133. (NACA Tech. Rep. N 1244.)

10. Townsend A.A. The structure of turbulent shear flow. 1st Ed. Cambridge: Cambridge Univ. Press, 1956.

11. Grant H.Z. The large eddies of turbulent motion // J. Fluid. Mech. 1957. V.4. P.149-190.

12. Rayne F.R., Lamley J.L. Large eddy structure of the turbulent wake behinde a circular cylinder // Phys.Fluids Suppl. 1967. V.10.P. 194-196.

13. Townsend A.A. Entrainment and the structure of turbulent flow // J. Fluid Mech. 1970. V.41. P.13-46.

14. Townsend A.A. The structure of turbulent shear flow. 2nd Ed. Cambridge: Cambridge Univ. Press, 1976.

15. Кадер Б.Л., Яглом А.М. Законы подобия для пристенных турбулентных течений. В сб. “Итоги науки и техн. ВИНИТИ. Сер. Механика жидкости и газа”, 1980, с. 81-185.

16. Kline J., Reynolds W.C., Schraub F.A., Runstadler P.W. The structure of turbulent boundary layers. // J. Fluid Mech. 1967. V. 30. P. 741-773.

17. Barenblatt G.I., Chorin A.J., Prostokishin V.M. A note on the intermediate region in turbulent boundary layers.// Phys. Fluids. 2000. V. 12. N.9. P. 2159-21-61.

18.  Rao K.N., Narasimha R., Narayanan M.A.B. Bursting in a turbulent boundary layer // J. Fluid Mech. 1971. V.48. P.339-352.

19. Grass A.J. Sructural features of turbulent flow over smooth and rough boundaries // J. Fluid Mech. 1971. V.50. P.223-256.

20. Blackwelder R.F., Eckelmann H. Sreamwise vortices associated with the bursting phenomenon // J. Fluid Mech. 1979. V.94. P.577-594.

21. Kovasnay L.S.G., Kibens V., Blackwelder R.F., Large scale motion in the intermitten region of a turbulent boundary layer // J. Fluid Mech. 1970. V.41. P.283-325.

22. Falco R.E. Coherent motions in the outer region of turbulent boundary layers // Phys. Fluids. 1977. V.20. N 10. P.5124-5132.

23. Blackwelder R.F., Kovasznay L.S.G. Time scale and correlation in a turbulent boundary layer // Phys. Fluids. 1972. V.15. P. 1545-1554.

24. Brown G.L, Thomas A.S.W. Large structure in a turbulent boundary layer // Phys. Fluids. 1977. V.20. N 10. P. 5243-5252.

25. Head M.R., Bandyopadhyay P. Combined flow visualization and hot wire measurements in turbulent boundary layer // Lehigh Workshop on Coherent Structure of Turbulent Boundary Layers / Ed. C.R. Smith, D.E. Abbott. 1978. P. 98-129.

26. Perry A.E., Lim T.T., Chong M.S., Teh E.W. The fabric of turbulence // AIAA Paper. 1980. N 80-1358.

27. Blackwelder R.F. Coherent structures associated with turbulent transport // Proc. 2nd Int. Sump.. On Transport Phenomena in Turbulent Flows. Tokyo, 1987. P.1-20.

28. Bogolepov V.V., Zharov V.A, Lipatov I.I., Khlopkov Yu.I. Model of a turbulent boundary layer with explicit identification of the coherent generation structure. Journal of Applied Mechanics and Technical Physics. Vol. 43, No. 4, pp. 544-551, 2002.

29. Садовский В.С., Синицина Н.П., Таганов Г.И. Численное исследование математической модели пристенного течения в турбулентном пограничном слое. В кн.: «Пристенные турбулентные течения.Ч.1» - Новосибирск. Изд. СЩ АН СССР. 1975.

30. Вигдорович И.И. Законы подобия для распределения скорости и компонент Тензора Рейнольдса в пристеночной области турбулентного пограничного слоя со вдувом и отсосом. Изв. РАН МЖГ, 2002, №5, с. 78-89.

31. Хлопков Ю.И., Жаров В.А., Горелов С.Л. Когерентные структуры в турбулентном пограничном слое. М.: МФТИ, 2002, 267с.

32. Cantwell B.J. Organized motion in flow. Ann. Rev. Fluid Mech. 1981. V.13. p.457-515.

33. M. Van Dyke. An album of fluid motion. Parabolic Press Stanford, California, 1982. 184p.

34. Fiedler H.E. Coherent structure. Advances in turbulence. Proc. of First European Turbulence Conference. Ed. G. Comte-Belo, J. Mathien. Lion, France, 1986. p.320-336.

35. Tadashi Utami, Totsuo Ueno. Experimental study on the coherent structure of turbulent open-channel flow using visualization and picture processing J. Fluid Mech. 1987. V. 175. p.399-440.

36. Acarlar M.S., Smith C.R. A study of hairpin vortices in a boundary layer. Part 2. Hairpin vortices generated by fluid injection. J. Fluid Mech. 1987. V.175. p.43-83.

37. Favre A.J., Gaviglio J.J., Dumas R. J. Fluid Mech. 1957, V.2, p. 313-341